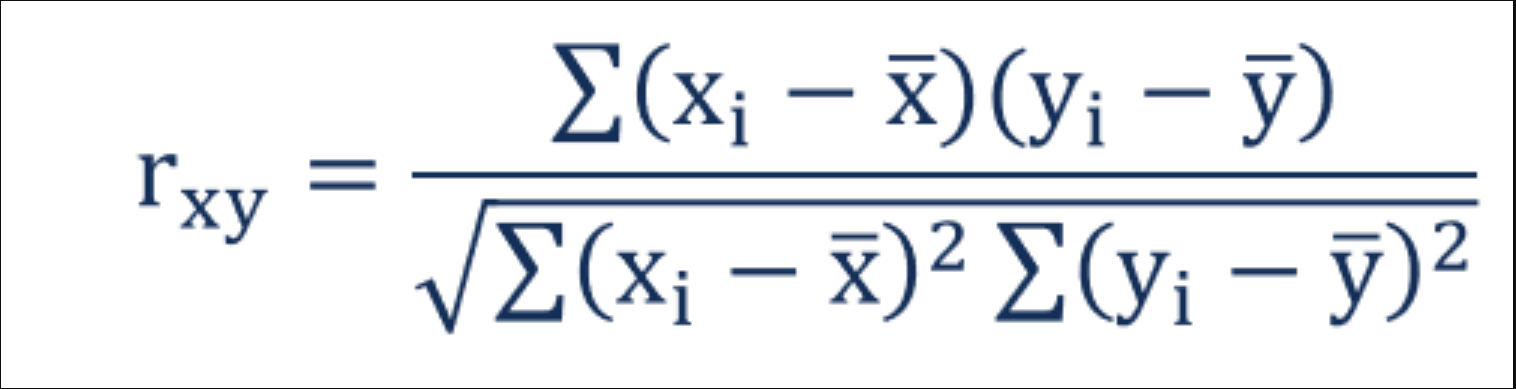
5  Correlation

5.1 What is Correlation?

  • The relationship between 2 variables
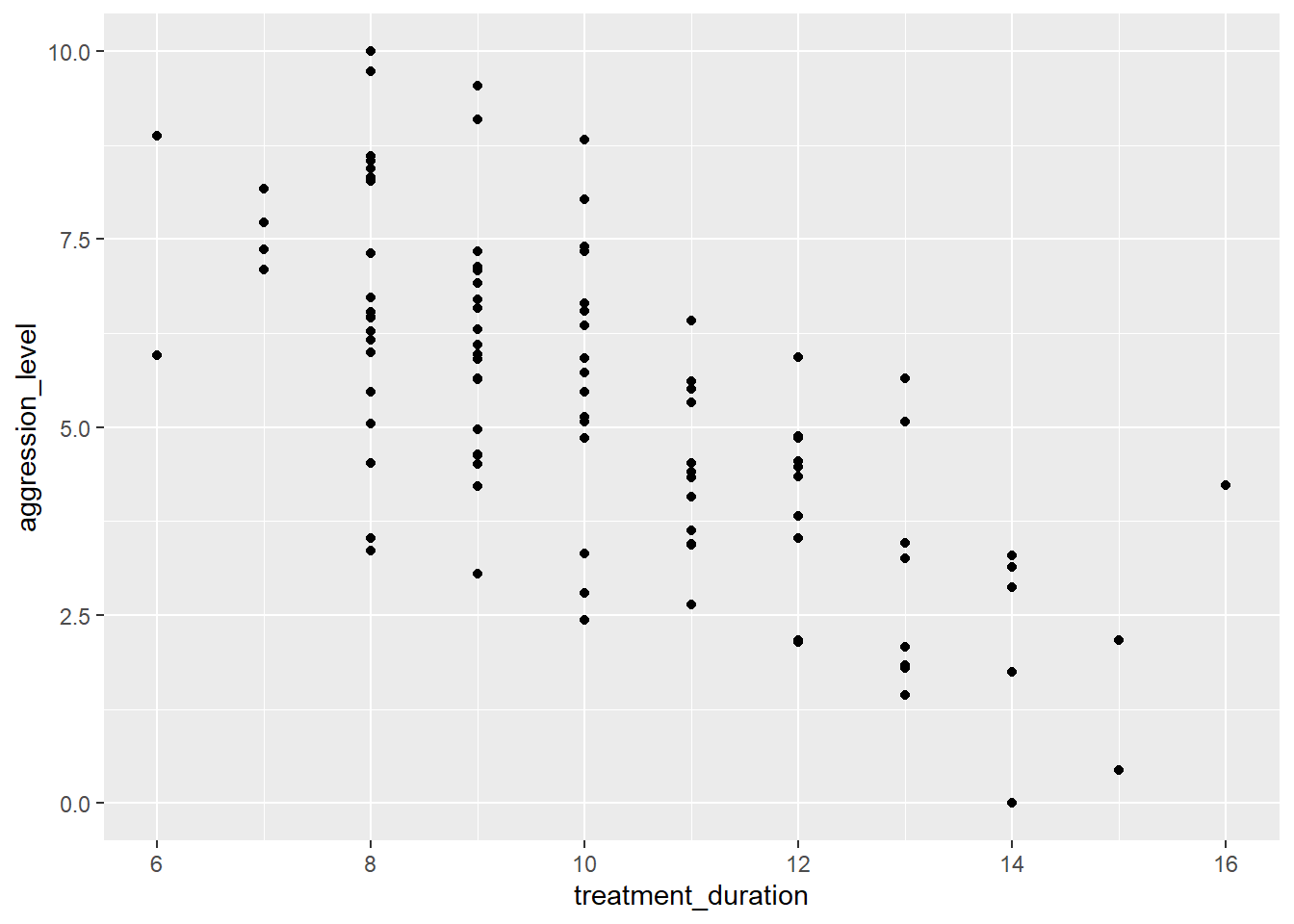
  • Question: Is treatment duration related to aggression levels?

5.2 How is correlation calculated?

  • Think of this as covariance divided by individual variance
  • If the changes are consistent with both variables, the final value will be higher

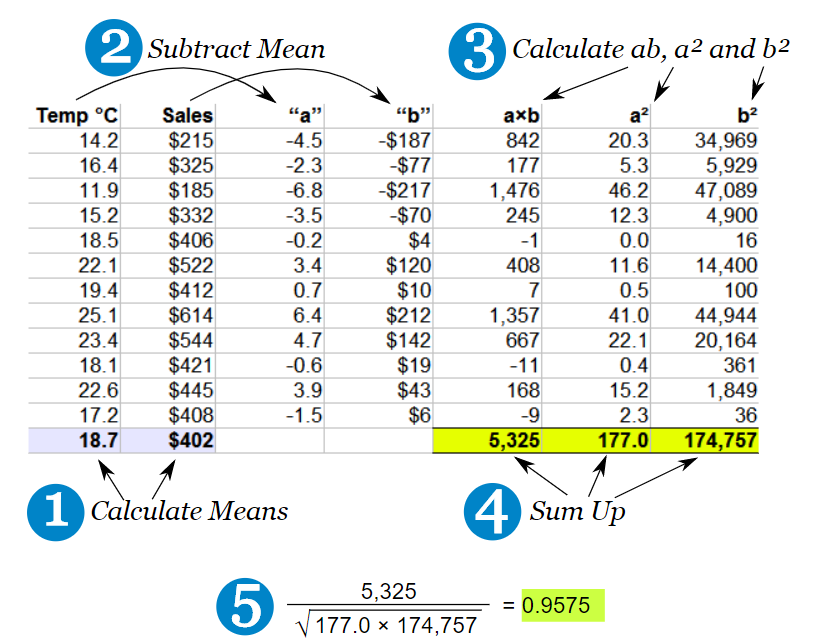
5.3 Running correlation in R

  • Step 1: Check assumptions
    • Data,distribution,linearity
  • Step 2: Run correlation
  • Step 3: Check R value
  • Step 4: Check significance

5.3.1 Check assumptions: data

  • Parametric tests require interval or ratio data
  • If the data are ordinal then a non-parametric correlation is used

What type of data are treatment duration and aggression level?

5.3.2 Check assumptions: distribution

  • Parametric tests require normally distributed data

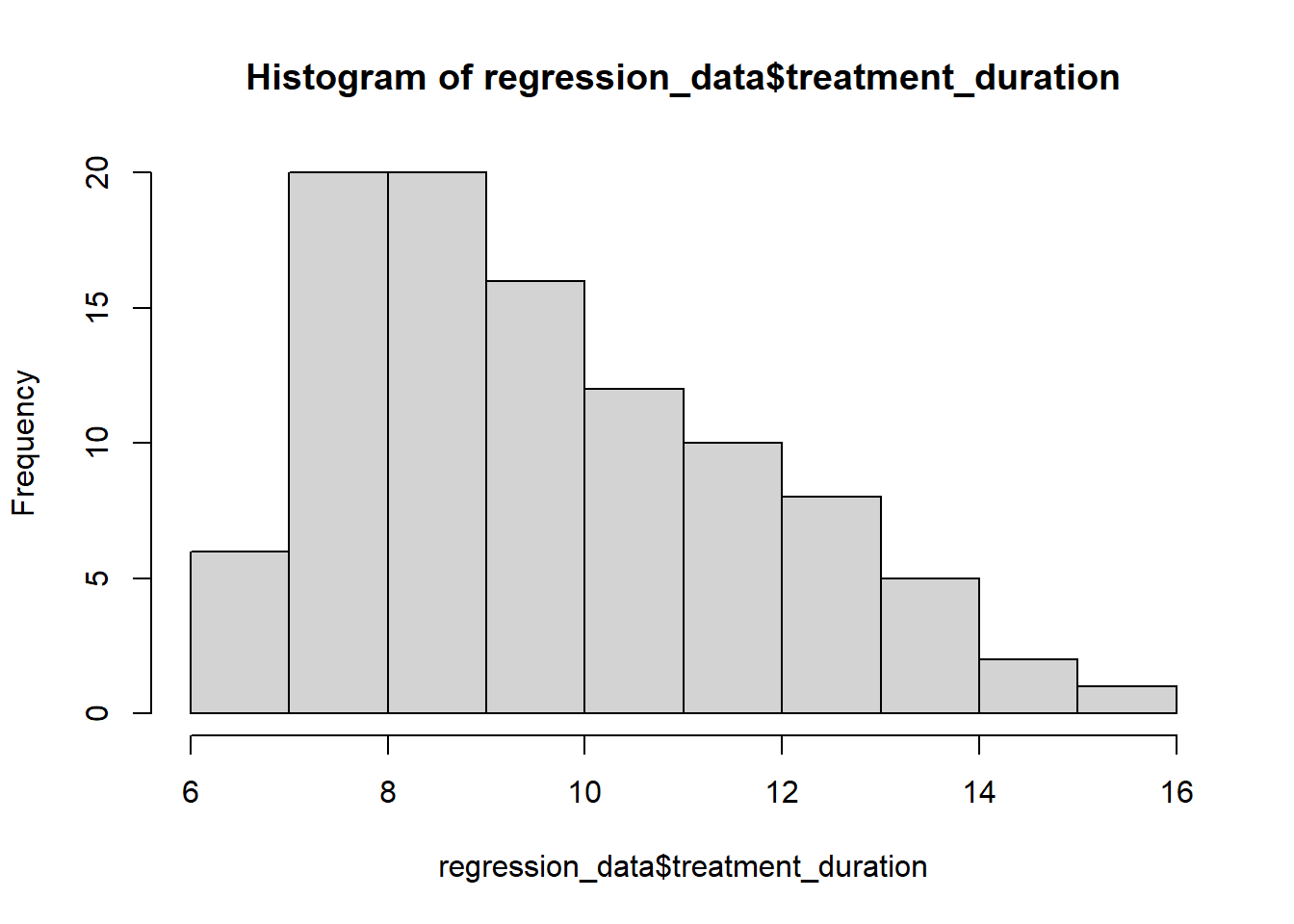
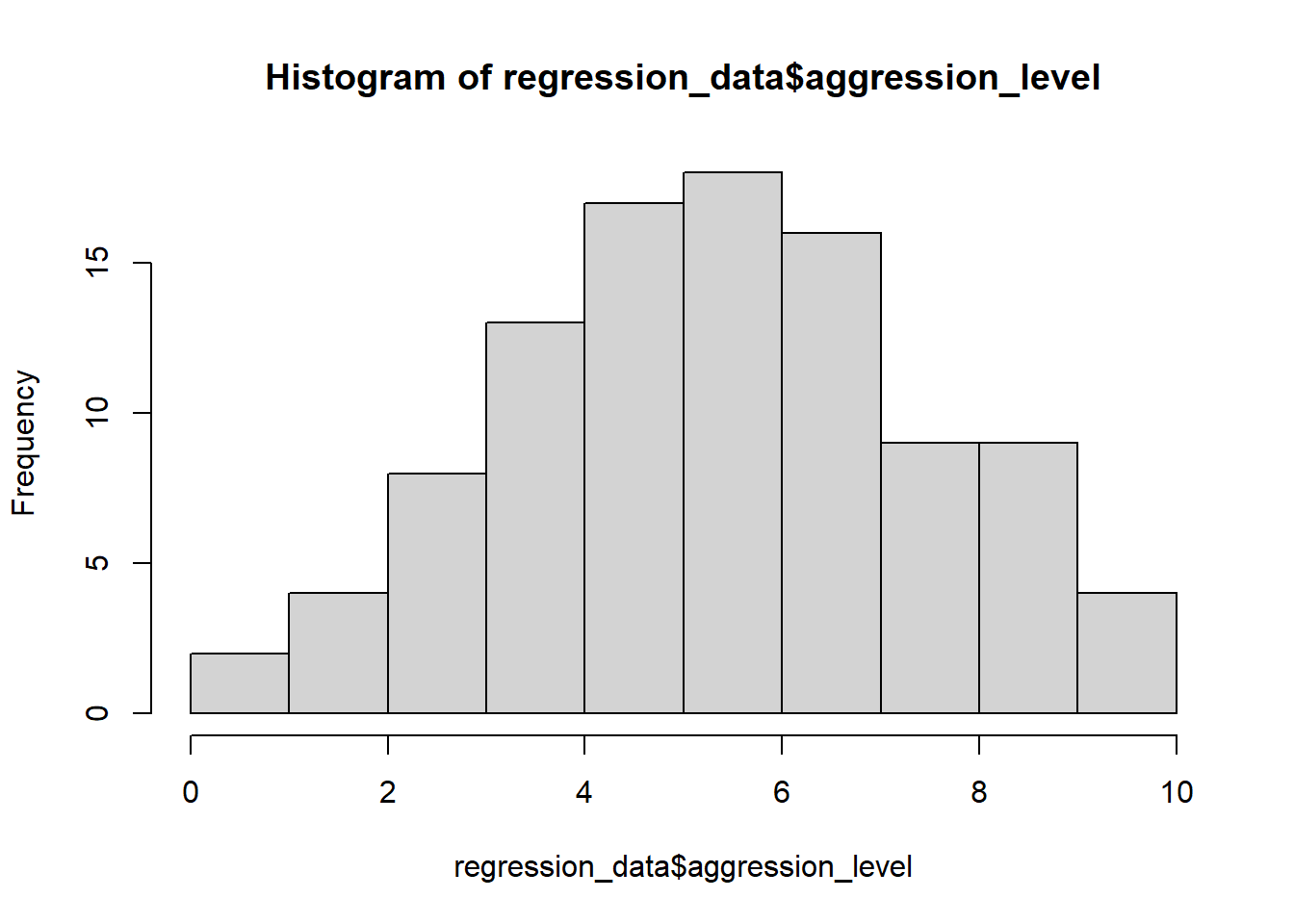
5.3.3 Check assumptions: distribution #2

  • Parametric tests require normally distributed data
shapiro.test(regression_data$treatment_duration)

    Shapiro-Wilk normality test

data:  regression_data$treatment_duration
W = 0.94971, p-value = 0.0007939
shapiro.test(regression_data$aggression_level)

    Shapiro-Wilk normality test

data:  regression_data$aggression_level
W = 0.9928, p-value = 0.8756
  • The normality assumption is less of an issue when sample size is > 30

5.3.4 Checking assumptions: linearity

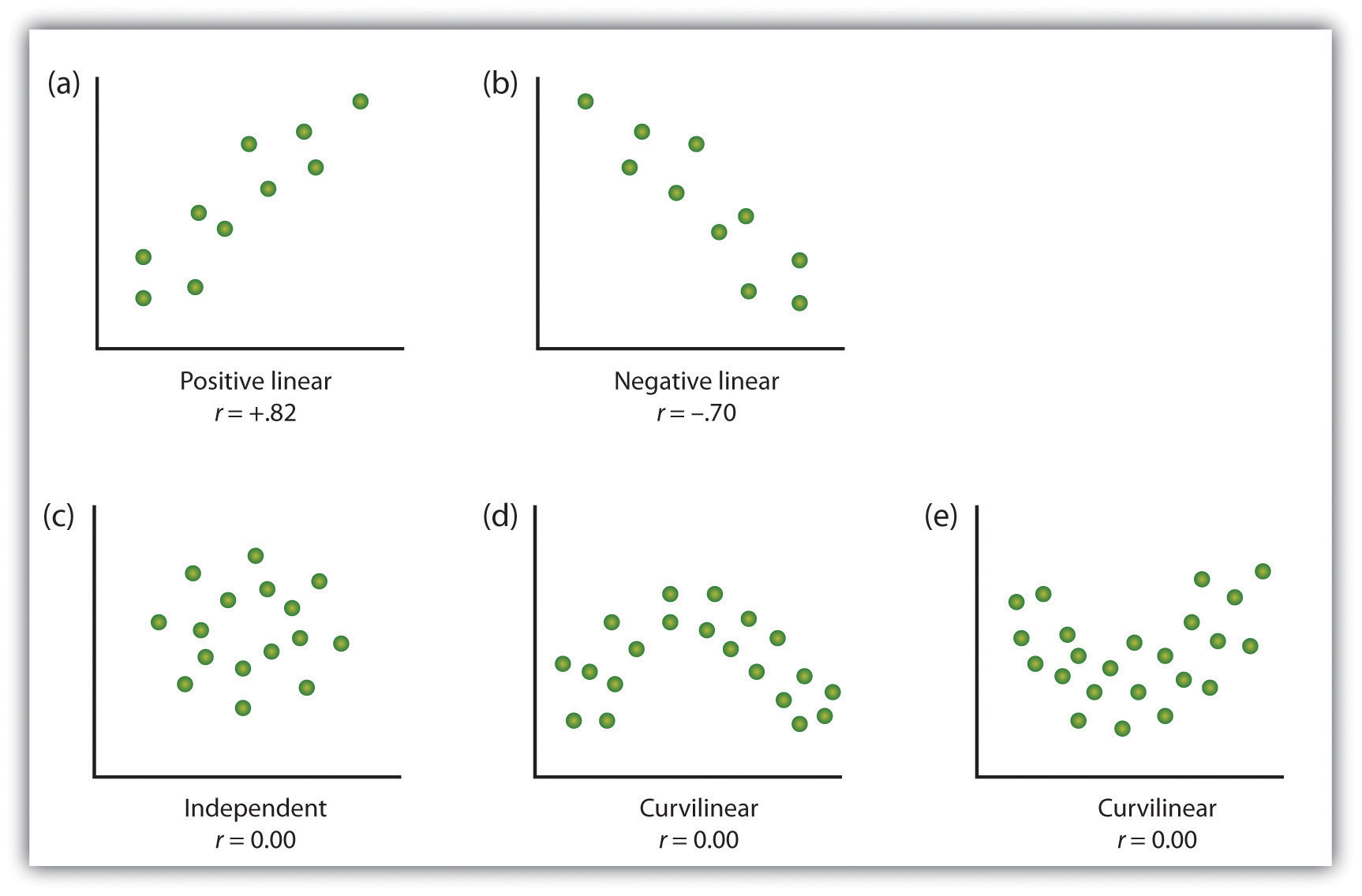
regression_data %>% ggplot(aes(x=treatment_duration,y=aggression_level)) +
  geom_point()

  • Here we are looking to see if the relationship is linear

5.3.5 Run correlation

  • R can run correlations using the cor.test() command
cor.test(regression_data$treatment_duration,regression_data$aggression_level)

    Pearson's product-moment correlation

data:  regression_data$treatment_duration and regression_data$aggression_level
t = -9.5503, df = 98, p-value = 1.146e-15
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.7838251 -0.5765006
sample estimates:
       cor 
-0.6942996

5.3.6 Check r Value (correlation value)

  • The r value tells us the strength and direction of the relationship
  • In the output it is labelled as “cor” (short for correlation)
cor.test(regression_data$treatment_duration,regression_data$aggression_level)

    Pearson's product-moment correlation

data:  regression_data$treatment_duration and regression_data$aggression_level
t = -9.5503, df = 98, p-value = 1.146e-15
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.7838251 -0.5765006
sample estimates:
       cor 
-0.6942996

5.3.7 Check the significance of the correlation

  • We can see that the significance by looking at the p value
    • The significance is 1.146^-15
    • This means: 0.0000000000000001146
  • Therefore p value < 0.05
cor.test(regression_data$treatment_duration,regression_data$aggression_level)

    Pearson's product-moment correlation

data:  regression_data$treatment_duration and regression_data$aggression_level
t = -9.5503, df = 98, p-value = 1.146e-15
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.7838251 -0.5765006
sample estimates:
       cor 
-0.6942996

6 Simple Regression

6.1 What is regression?

  • Testing to see if we can make predictions based on data that are correlated

We found a strong correlation between treatment duration and agression levels. Can we use this data to predict aggression levels of other clients, based on their treatment duration?

  • When we carry out regression, we get a information about:
    • How much variance in the outcome is explained by the predictor
    • How confident we can be about these results generalising (i.e. significance)
    • How much error we can expect from anu predictions that we make (i.e. standard error of the estimate)
    • The figures we need to calculate a predicted outcome value (i.e. coefficient values)

6.2 How is regression calculated?

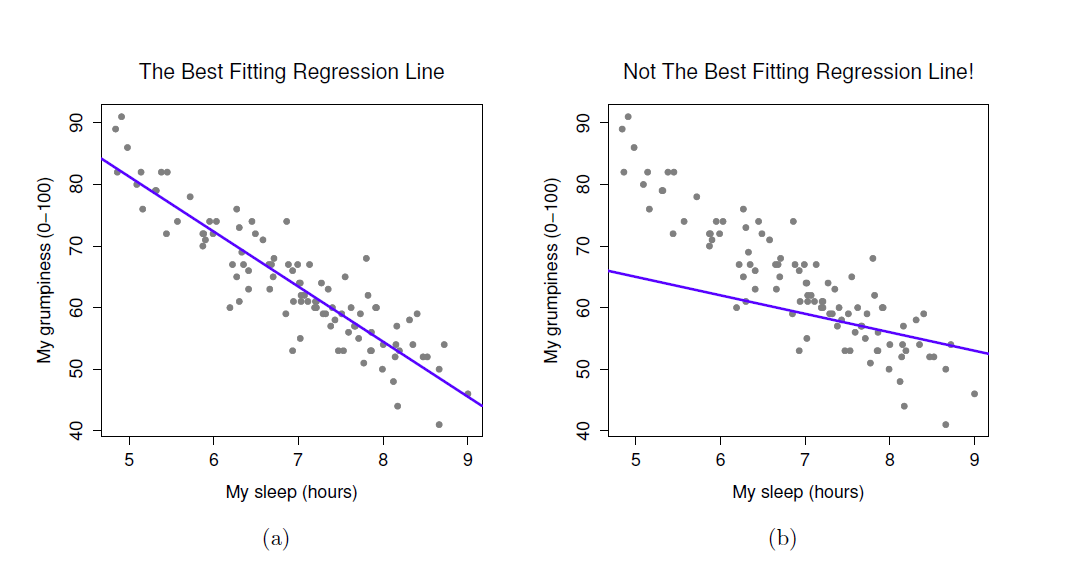
  • When we run a regression analysis, a calculation is done to select the “line of best fit”
  • This is a “prediction line” that minimises the overall amount of error
    • Error = difference between the data points and the line

6.3 The regression equation

  • Once the line of best fit is calculated, predictions are based on this line

  • To make predictions we need the intercept and slope of the line

    • Intercept or constant= where the line crosses the y axis
    • Slope or beta = the angle of the line

  • Predictions are made using the calculation for a line: Y = bX + c

  • You can think of the equation like this:

predicted outcome value = beta coefficient * value of predictor + constant

6.4 Running regression in R

  • Step 1: Run regression
  • Step 2: Check assumptions
    • Data
    • Distribution
    • Linearity
    • Homogeneity of variance
    • Uncorrelated predictors
    • Indpendence of residuals
    • No influental cases / outliers
  • Step 3: Check R^2 value
  • Step 4: Check model significance
  • Step 5: Check coefficient values

6.5 Run regression

  • We use the lm() command to run regression while saving the results
  • We then use the summary() function to check the results
model1 <- lm(formula= aggression_level ~ treatment_duration ,data=regression_data)
summary(model1)

Call:
lm(formula = aggression_level ~ treatment_duration, data = regression_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.4251 -1.1493 -0.0593  0.8814  3.4542 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         12.3300     0.7509   16.42  < 2e-16 ***
treatment_duration  -0.6933     0.0726   -9.55 1.15e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.551 on 98 degrees of freedom
Multiple R-squared:  0.4821,    Adjusted R-squared:  0.4768 
F-statistic: 91.21 on 1 and 98 DF,  p-value: 1.146e-15

6.6 What are residuals?

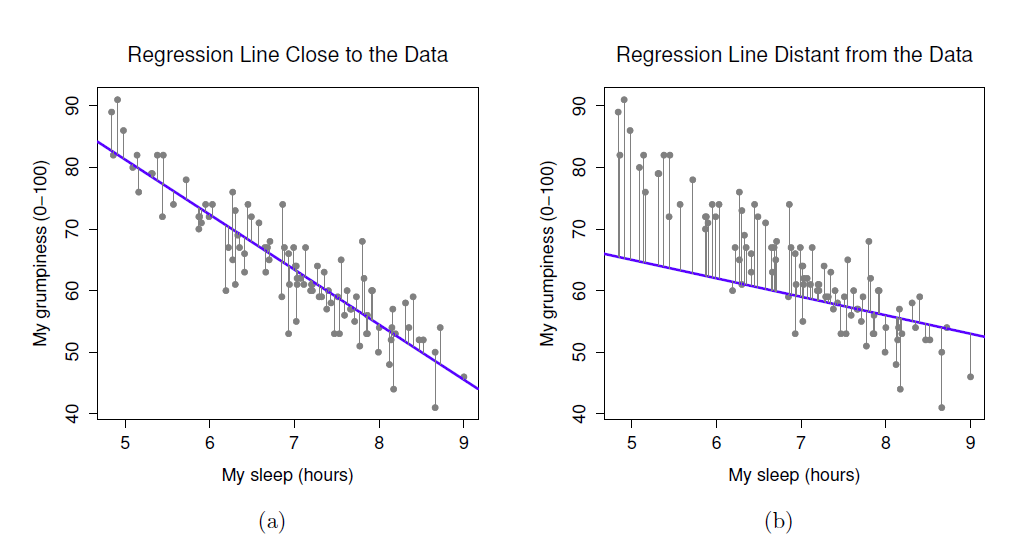
  • In regression, the assumptions apply to the residuals, not the data themselves
  • Residual just means the difference between the data point and the regression line

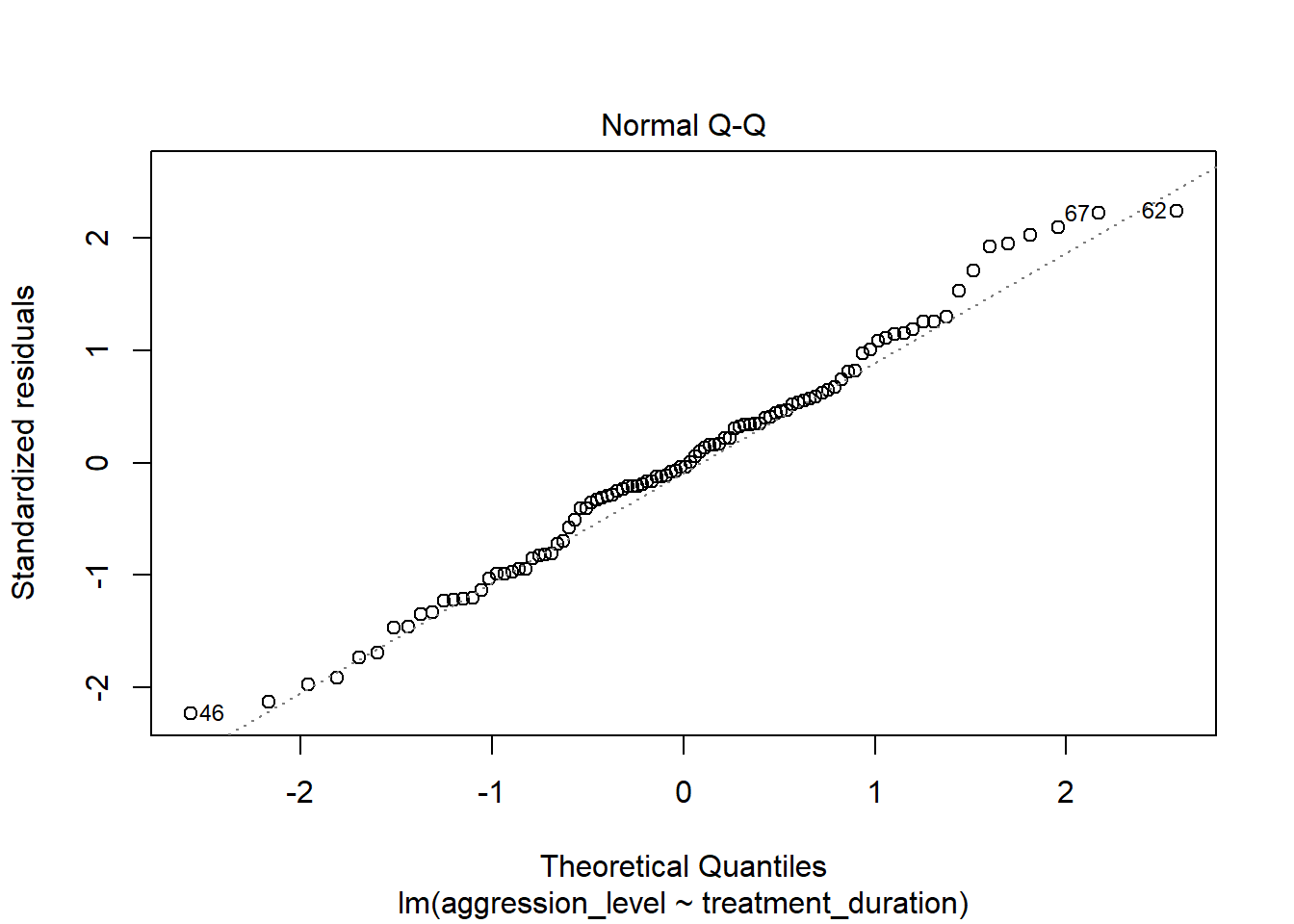
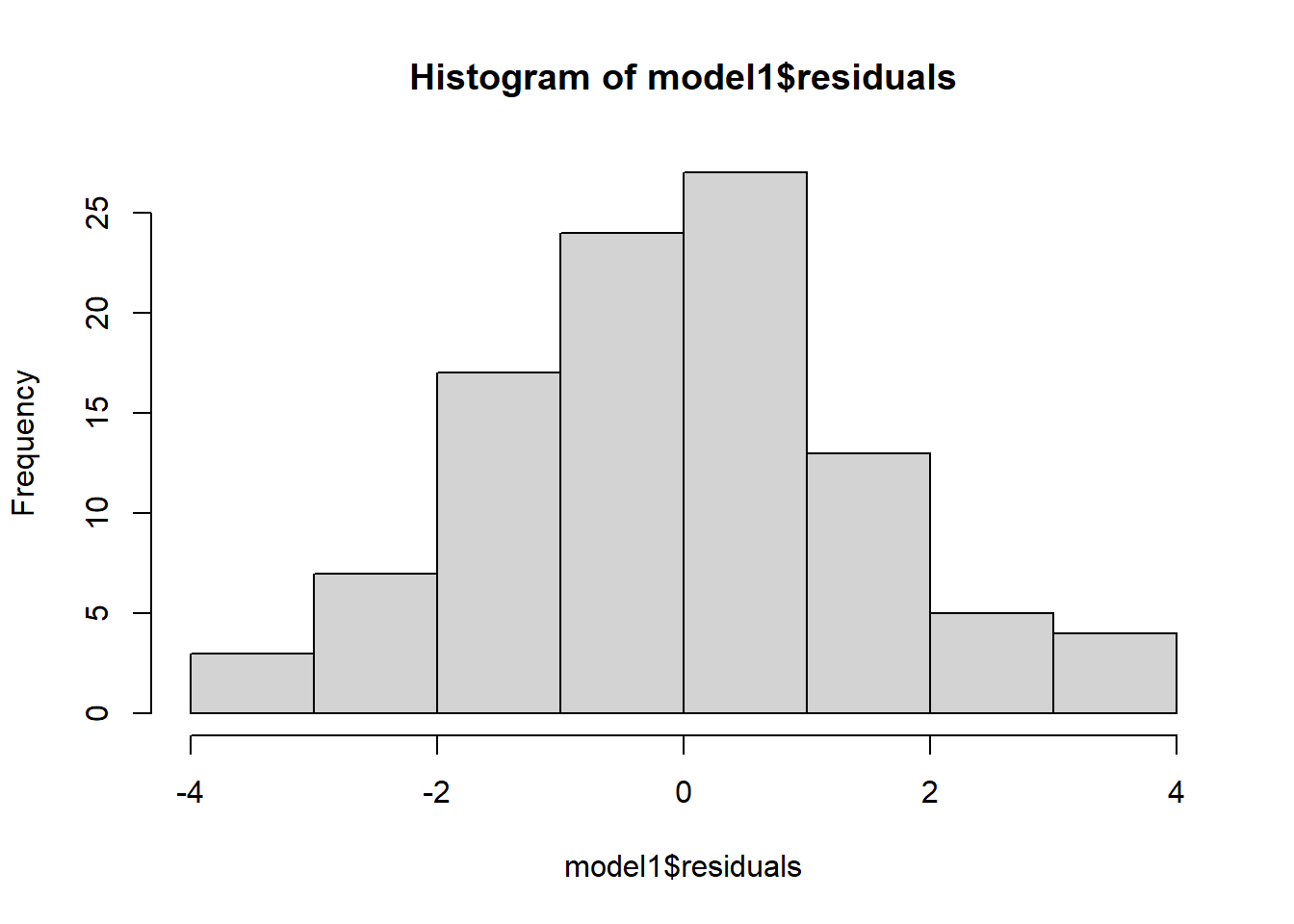
6.7 Check assumptions: distribution

  • Using the plot() command on our regression model will give us some useful diagnostic plots
  • The second plot that it outputs shows the normality
plot(model1, which=2)

  • We could also use a histogram to check the distribution
  • Notice how we can use the $ sign to get the residuals from the model
hist(model1$residuals)

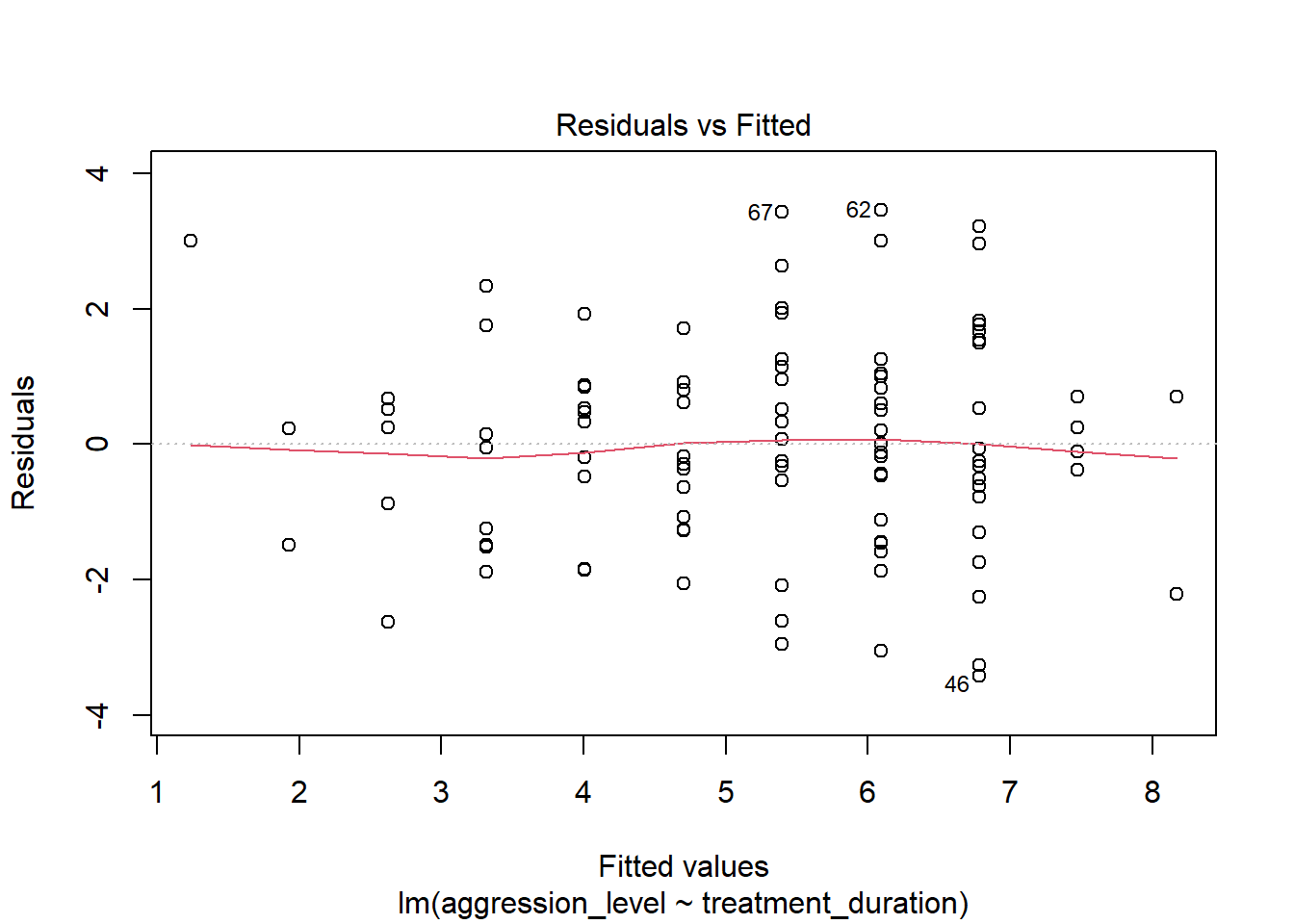
6.8 Check assumptions: linearity

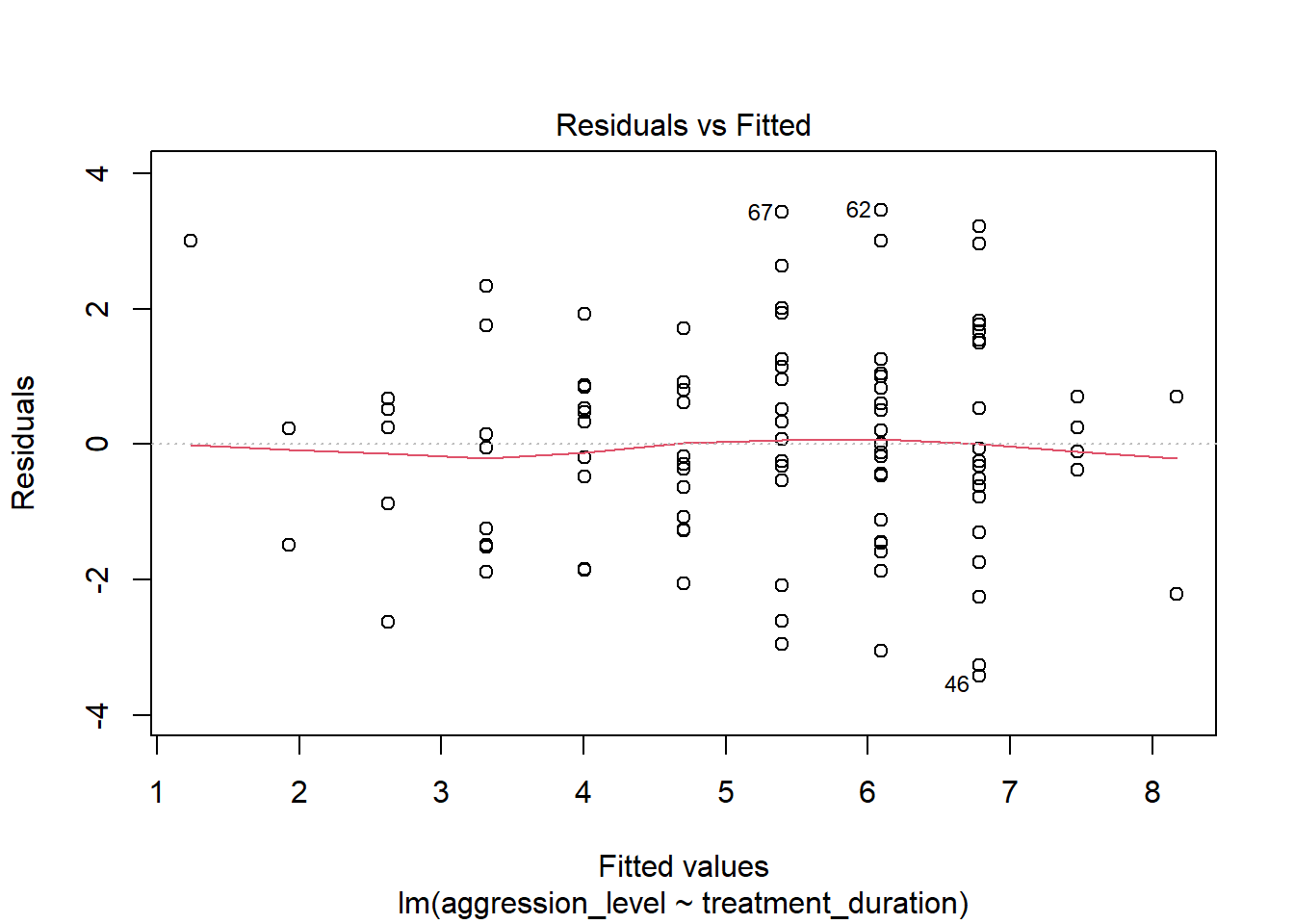
  • Using the plot() command on our regression model will give us some useful diagnostic plots
  • The first plot that it outputs shows the residuals vs the fitted values
  • Here, we want to see them spread out, with the line being horizontal and straight
plot(model1, which=1)

  • There is a slight amount of curvilinearity here but nothing to be worried about

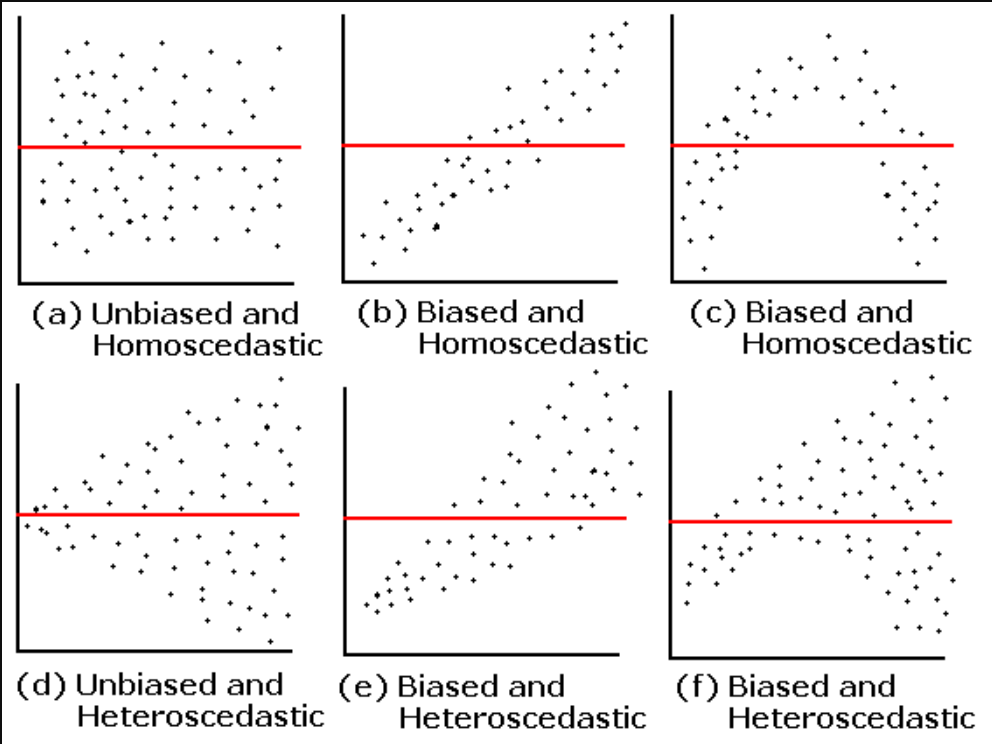
6.9 Check assumptions: Homogeneity of Variance #1

  • We can use the sample plot to check Homogeneity of Variance
  • We want the variance to be constant across the data set. We do not want the variance to change at different points in the data
plot(model1, which=1)

  • A violation of Homogeneity of Variance would usually look like a funnel, with the data narrowing

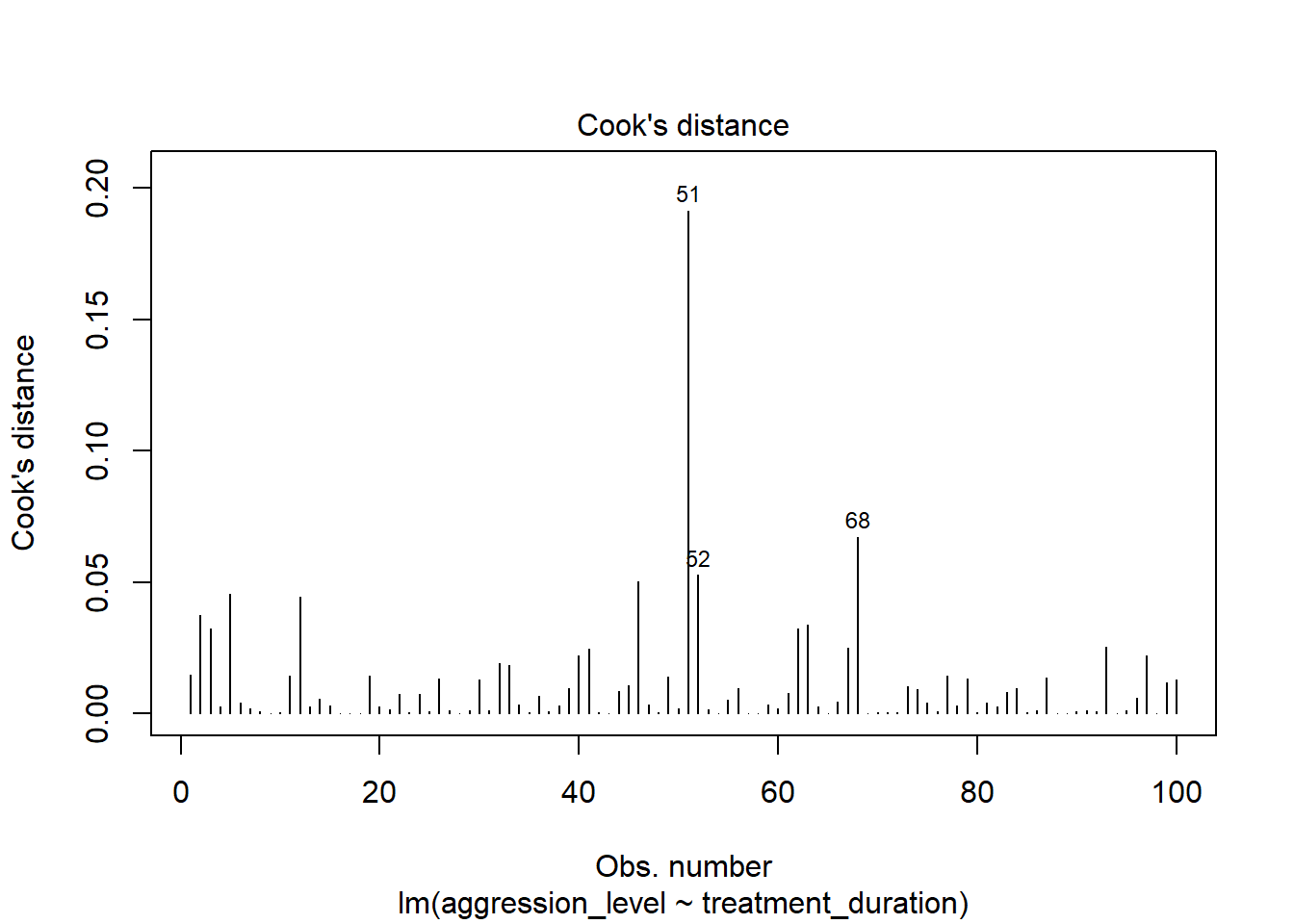
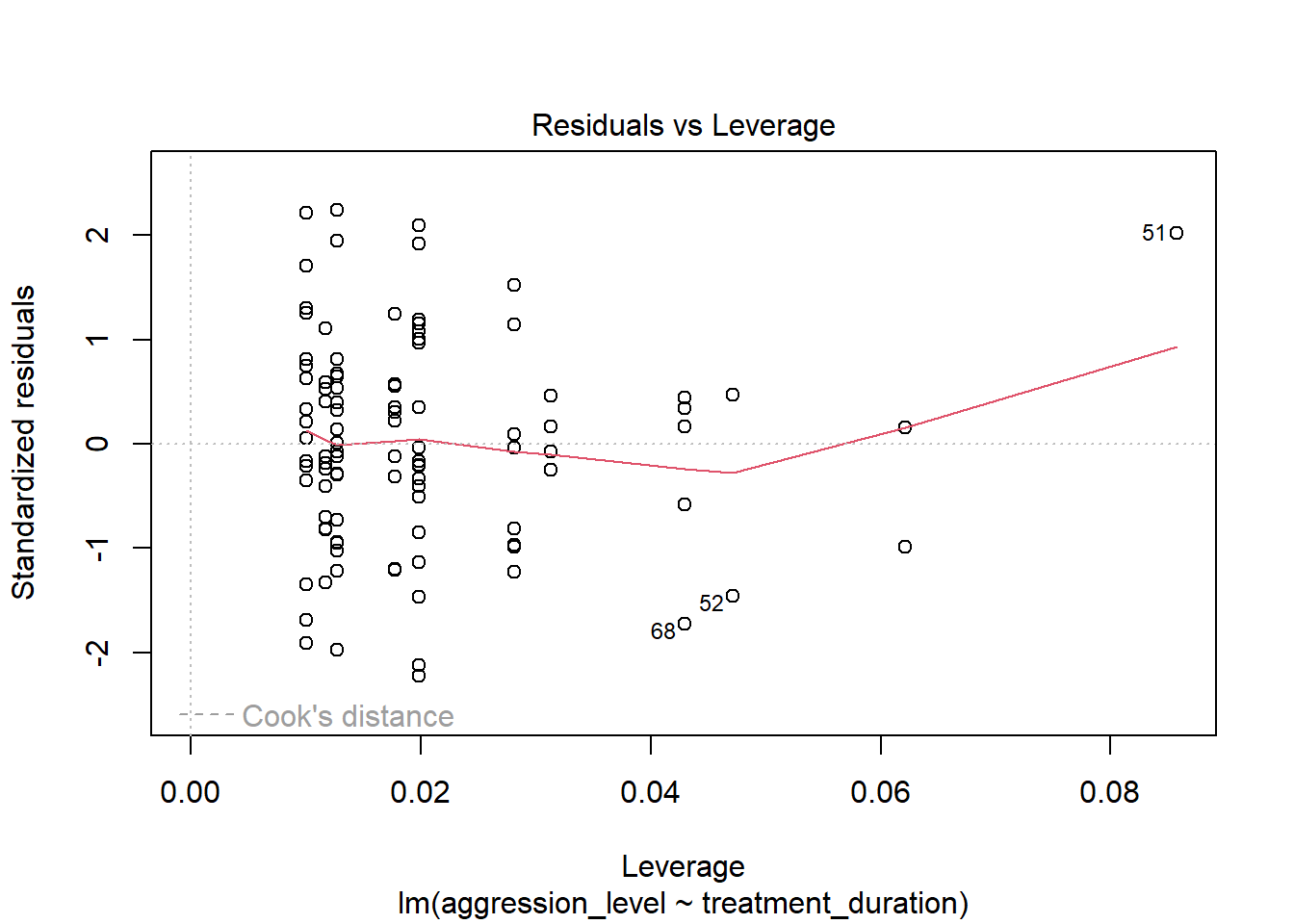
6.10 Check assumptions: Influential cases

  • We need to check that there are no extreme outliers - they could throw off our predictions
  • We are looking for participants that have high rediduals + high leverage
    • Some guidance suggests anything higher than 1 is an influential case
    • Others suggest 4/n is the cut off point (4 divided by number of participants)
plot(model1, which=4)

  • We are looking for participants that have high rediduals + high leverage
    • No cases over 1
    • Many are over 0.04 (4/n = 0.04)
plot(model1, which=5)

6.11 Check the r squared value

  • r^2 = the amount of variance in the outcome that is explained by the predictor(s)
  • The closer this value is to 1, the more useful our regression model is for predicting the outcome
modelSummary <- summary(model1)
modelSummary

Call:
lm(formula = aggression_level ~ treatment_duration, data = regression_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.4251 -1.1493 -0.0593  0.8814  3.4542 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         12.3300     0.7509   16.42  < 2e-16 ***
treatment_duration  -0.6933     0.0726   -9.55 1.15e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.551 on 98 degrees of freedom
Multiple R-squared:  0.4821,    Adjusted R-squared:  0.4768 
F-statistic: 91.21 on 1 and 98 DF,  p-value: 1.146e-15
  • The r^2 of 0.482052 means that 48% of the variance in aggression level is explained by treatment duration

6.12 Check model significance

  • The model significance is displayed at the very end of the output
    • p-value: 1.146e-15
    • As p < 0.05, the model is significant
modelSummary

Call:
lm(formula = aggression_level ~ treatment_duration, data = regression_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.4251 -1.1493 -0.0593  0.8814  3.4542 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         12.3300     0.7509   16.42  < 2e-16 ***
treatment_duration  -0.6933     0.0726   -9.55 1.15e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.551 on 98 degrees of freedom
Multiple R-squared:  0.4821,    Adjusted R-squared:  0.4768 
F-statistic: 91.21 on 1 and 98 DF,  p-value: 1.146e-15

6.13 Check coefficient values

  • The coefficient values are displayed in the coefficients table
  • If we have more than one predictor, they are all listed here
modelSummary$coefficients
                     Estimate Std. Error   t value     Pr(>|t|)
(Intercept)        12.3300211 0.75087601 16.420848 6.840516e-30
treatment_duration -0.6933201 0.07259671 -9.550297 1.145898e-15
  • The beta coefficient for treatment duration is in the Estimate column
  • For every unit increase in treatment duration, aggression level decreases by 0.69

6.14 The regression equation

  • The regression equation is:

Outcome = predictor value * beta coefficient + constant

  • For this model, that is:

Aggression level = treatment duration * -0.69 + 12.33

modelSummary$coefficients
                     Estimate Std. Error   t value     Pr(>|t|)
(Intercept)        12.3300211 0.75087601 16.420848 6.840516e-30
treatment_duration -0.6933201 0.07259671 -9.550297 1.145898e-15

6.15 Accounting for error in predictions

  • We also know that the accuracy of predictions will be within a certain margin of error
  • This is known as standard error of the estimate or residual standard error 
modelSummary

Call:
lm(formula = aggression_level ~ treatment_duration, data = regression_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.4251 -1.1493 -0.0593  0.8814  3.4542 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         12.3300     0.7509   16.42  < 2e-16 ***
treatment_duration  -0.6933     0.0726   -9.55 1.15e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.551 on 98 degrees of freedom
Multiple R-squared:  0.4821,    Adjusted R-squared:  0.4768 
F-statistic: 91.21 on 1 and 98 DF,  p-value: 1.146e-15