3  Exploratory and descriptive analysis with R

3.1 Working example - record sales data

Let’s import the data

Album_Sales <- read.csv("datasets/album_sales.csv")

Let’s look at the data

head(Album_Sales)
Adverts Sales Airplay Attract Genre
10.256 330 43 10 Country
985.685 120 28 7 Pop
1445.563 360 35 7 HipHop
1188.193 270 33 7 HipHop
574.513 220 44 5 Metal
568.954 170 19 5 Country

3.2 Let’s make sure our data types are correct #1

  • This variable is currently stored as charcters, not as a factor / category variable
str(Album_Sales$Genre) 
 chr [1:200] "Country" "Pop" "HipHop" "HipHop" "Metal" "Country" "Pop" ...
  • We can save it as a factor
Album_Sales$Genre <- as.factor(Album_Sales$Genre)

str(Album_Sales$Genre) 
 Factor w/ 4 levels "Country","HipHop",..: 1 4 2 2 3 1 4 4 3 2 ...

3.3 Measures of central tendency

The main measures of central tendency are: - Mean - Median - Mode

3.3.1 Mean

“What is the mean of album sales?”

mean(Album_Sales$Sales)
[1] 193.2

3.3.2 Trimmed mean

  • The trimmed mean is used to reduce the influence of outliers on the summary
mean(Album_Sales$Sales, trim = 0.05)
[1] 192.6667

3.3.3 Median

“What is the median amount of Airplay?”

median(Album_Sales$Airplay)
[1] 28

3.3.4 Mode

“What is the most common attractiveness rating of bands?”

  • The easiest way to get the mode in R is to generate a frequency table
table(Album_Sales$Attract)

 1  2  3  4  5  6  7  8  9 10 
 3  1  1  4 17 44 73 44 12  1
  • We can then look for the most frequently occuring response

3.4 Measures of dispresion or variance

3.4.1 Range

The range is the difference between the lowest and highest values

  • You can calculate it using these values
max(Album_Sales$Airplay) - min(Album_Sales$Airplay)
[1] 63
  • Or you can use the range command to get the min and max values in one go
range(Album_Sales$Airplay)
[1]  0 63

3.4.2 Interquartile range

  • We know that the median is the “middle” of the data = 50th percentile
  • The interquatile range is the difference between the values at the 25th and 75th percentiles
quantile( x = Album_Sales$Airplay, probs = c(.25,.75) )
  25%   75% 
19.75 36.00
  • Interquartile range = 36 - 19.75 = 16.25

Sum of squares

  • The difference between each value and the mean value, squared, and then summed together
sum( (Album_Sales$Adverts - mean(Album_Sales$Adverts))^2 )
[1] 46936335

3.4.3 Variance

  • Variance: Sum of sqaures divided by n-1
# variance calculation
varianceAdverts <- sum( (Album_Sales$Adverts - mean(Album_Sales$Adverts))^2 ) / 199

3.4.4 Standard deviation

  • Standard deviation is square root of the variance
# sd calculation


sqrt(varianceAdverts)
[1] 485.6552
  • Can be calculated using the sd() command
sd(Album_Sales$Adverts)
[1] 485.6552

3.5 Skewness and Kurtosis

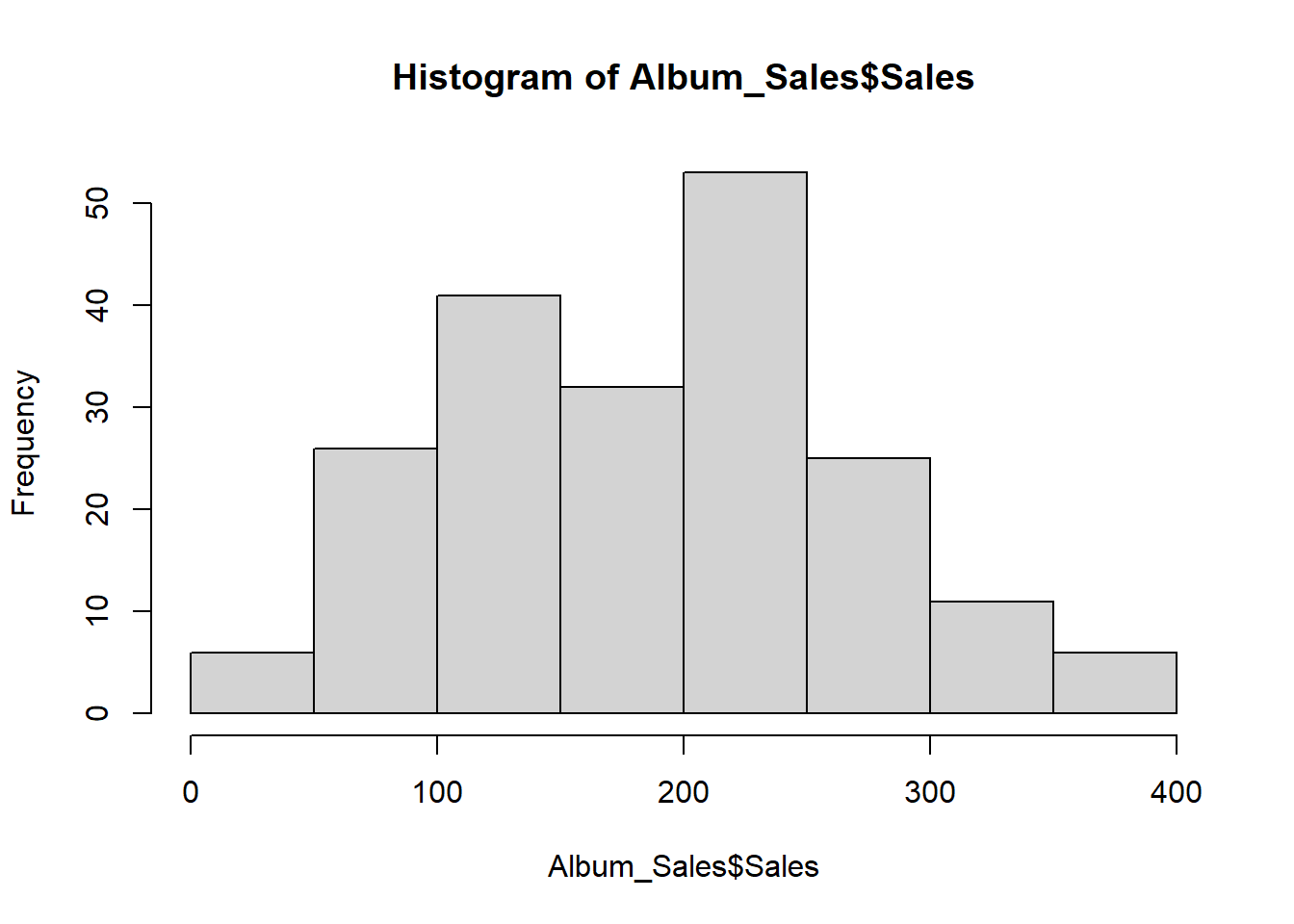
3.5.1 Assessing skewness of distribution #1

  • It is possible to use graphs to view the distribution
  • We will focus on graphic presentation of data next week
hist(Album_Sales$Sales)

3.5.2 Assessing skewness of distribution #2

  • We can check raw skewness value using the skew() command in the psych package
library(psych)
Warning: package 'psych' was built under R version 4.2.3

Attaching package: 'psych'
The following object is masked from 'package:car':

    logit
The following objects are masked from 'package:ggplot2':

    %+%, alpha
skew(Album_Sales$Sales)
[1] 0.0432729

3.5.3 Kurtosis

informal term technical name kurtosis value
“too flat” platykurtic negative
“just pointy enough” mesokurtic zero
“too pointy” leptokurtic positive 
kurtosi(Album_Sales$Sales)
[1] -0.7157339

3.5.4 Assessing normality of distribution

  • We can use the shapiro-wilk test of normality
  • This is part of “base” r (no package needed)
shapiro.test(Album_Sales$Sales)

    Shapiro-Wilk normality test

data:  Album_Sales$Sales
W = 0.98479, p-value = 0.02965

3.6 Getting and overall summary

3.6.1 summary() - in “base R”

summary(Album_Sales)
    Adverts             Sales          Airplay         Attract     
 Min.   :   9.104   Min.   : 10.0   Min.   : 0.00   Min.   : 1.00  
 1st Qu.: 215.918   1st Qu.:137.5   1st Qu.:19.75   1st Qu.: 6.00  
 Median : 531.916   Median :200.0   Median :28.00   Median : 7.00  
 Mean   : 614.412   Mean   :193.2   Mean   :27.50   Mean   : 6.77  
 3rd Qu.: 911.226   3rd Qu.:250.0   3rd Qu.:36.00   3rd Qu.: 8.00  
 Max.   :2271.860   Max.   :360.0   Max.   :63.00   Max.   :10.00  
     Genre   
 Country:46  
 HipHop :53  
 Metal  :48  
 Pop    :53

3.6.2 describe() - in the “psych” package #1

describe(Album_Sales)
vars n mean sd median trimmed mad min max range skew kurtosis se
Adverts 1 200 614.4123 485.655208 531.916 560.80516 489.0882 9.104 2271.86 2262.756 0.8399360 0.1687385 34.3410091
Sales 2 200 193.2000 80.698957 200.000 192.68750 88.9560 10.000 360.00 350.000 0.0432729 -0.7157339 5.7062779
Airplay 3 200 27.5000 12.269585 28.000 27.46250 11.8608 0.000 63.00 63.000 0.0588275 -0.0924910 0.8675907
Attract 4 200 6.7700 1.395290 7.000 6.88125 1.4826 1.000 10.00 9.000 -1.2668371 3.5555040 0.0986619
Genre* 5 200 2.5400 1.115627 3.000 2.55000 1.4826 1.000 4.00 3.000 -0.0242500 -1.3661364 0.0788867

3.6.3 describe() - in the “psych” package #2

  • We can describe by factor variables
describeBy(Album_Sales, group = Album_Sales$Genre)

 Descriptive statistics by group 
group: Country
        vars  n   mean     sd median trimmed    mad  min     max   range  skew
Adverts    1 46 656.22 507.96 574.14  620.40 581.96  9.1 1985.12 1976.01  0.51
Sales      2 46 201.74  73.64 210.00  200.79  66.72 60.0  360.00  300.00  0.03
Airplay    3 46  29.07  10.53  28.00   28.50  11.12  9.0   54.00   45.00  0.44
Attract    4 46   6.52   1.63   7.00    6.71   1.48  1.0   10.00    9.00 -1.49
Genre*     5 46   1.00   0.00   1.00    1.00   0.00  1.0    1.00    0.00   NaN
        kurtosis    se
Adverts    -0.65 74.89
Sales      -0.52 10.86
Airplay    -0.10  1.55
Attract     3.54  0.24
Genre*       NaN  0.00
------------------------------------------------------------ 
group: HipHop
        vars  n   mean     sd median trimmed    mad   min  max   range  skew
Adverts    1 53 606.32 452.84 601.43  568.33 501.36 10.65 2000 1989.35  0.70
Sales      2 53 199.62  92.71 200.00  200.70 103.78 10.00  360  350.00 -0.10
Airplay    3 53  28.09  13.86  30.00   28.33  14.83  0.00   55   55.00 -0.14
Attract    4 53   6.96   1.13   7.00    7.00   1.48  3.00    9    6.00 -0.80
Genre*     5 53   2.00   0.00   2.00    2.00   0.00  2.00    2    0.00   NaN
        kurtosis    se
Adverts     0.05 62.20
Sales      -0.91 12.74
Airplay    -0.83  1.90
Attract     2.03  0.15
Genre*       NaN  0.00
------------------------------------------------------------ 
group: Metal
        vars  n   mean     sd median trimmed    mad  min     max   range  skew
Adverts    1 48 693.45 534.06  593.0  640.19 521.34 45.3 2271.86 2226.56  0.92
Sales      2 48 197.71  75.18  200.0  198.25  88.96 40.0  340.00  300.00 -0.07
Airplay    3 48  27.96  11.37   27.5   28.00  11.12  2.0   57.00   55.00  0.02
Attract    4 48   6.85   1.34    7.0    6.90   1.48  2.0    9.00    7.00 -0.84
Genre*     5 48   3.00   0.00    3.0    3.00   0.00  3.0    3.00    0.00   NaN
        kurtosis    se
Adverts     0.21 77.08
Sales      -0.94 10.85
Airplay    -0.26  1.64
Attract     1.74  0.19
Genre*       NaN  0.00
------------------------------------------------------------ 
group: Pop
        vars  n   mean     sd median trimmed    mad   min     max   range  skew
Adverts    1 53 514.63 446.04  429.5  453.85 438.01 15.31 1789.66 1774.35  1.01
Sales      2 53 175.28  77.92  160.0  171.86  88.96 40.00  360.00  320.00  0.34
Airplay    3 53  25.13  12.75   26.0   25.02  11.86  1.00   63.00   62.00  0.25
Attract    4 53   6.72   1.47    7.0    6.81   1.48  1.00    9.00    8.00 -1.11
Genre*     5 53   4.00   0.00    4.0    4.00   0.00  4.00    4.00    0.00   NaN
        kurtosis    se
Adverts     0.27 61.27
Sales      -0.67 10.70
Airplay     0.46  1.75
Attract     2.51  0.20
Genre*       NaN  0.00

3.7 Basic statistical tests (more detail in later sections)

3.7.1 Corrleation

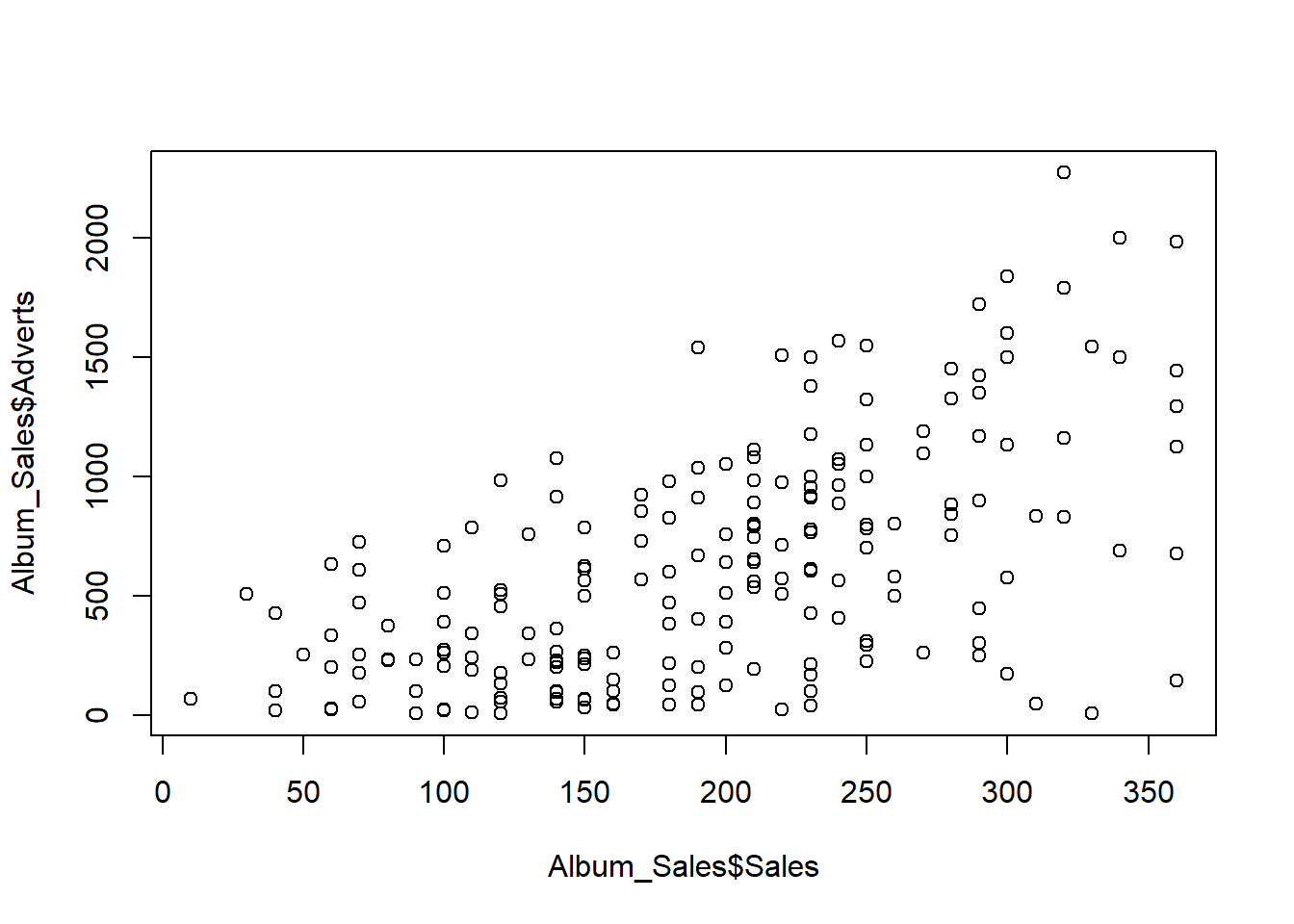
“Is there a relationship between advert spend and sales?”

  • We would use an correlational analysis to answer this question
plot(Album_Sales$Sales,Album_Sales$Adverts)

“Is there a relationship between advert spend and sales?”

  • We would use an correlational analysis to answer this question
cor.test(Album_Sales$Sales,Album_Sales$Adverts)

    Pearson's product-moment correlation

data:  Album_Sales$Sales and Album_Sales$Adverts
t = 9.9793, df = 198, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.4781207 0.6639409
sample estimates:
      cor 
0.5784877

3.7.2 Tests of difference - t-test

“Is there a significant difference in sales between the Country and Hip-hop musical genres?”

  • We would use a t-test to answer this question
myTtestData <- Album_Sales %>% filter(Genre == c("Country", "HipHop"))

t.test(myTtestData$Sales ~ myTtestData$Genre)

    Welch Two Sample t-test

data:  myTtestData$Sales by myTtestData$Genre
t = 0.80489, df = 40.62, p-value = 0.4256
alternative hypothesis: true difference in means between group Country and group HipHop is not equal to 0
95 percent confidence interval:
 -27.80146  64.62904
sample estimates:
mean in group Country  mean in group HipHop 
             216.0000              197.5862

3.7.3 Tests of difference - ANOVA

“Is there a significant difference in sales between all musical genres?”

  • We would use an ANOVA to answer this question
myAnova <- aov(Album_Sales$Sales ~ Album_Sales$Genre)
summary(myAnova)
                   Df  Sum Sq Mean Sq F value Pr(>F)
Album_Sales$Genre   3   23530    7843   1.208  0.308
Residuals         196 1272422    6492