Topic 7 Correlation

7.1 What is Correlation?

  • The relationship between 2 variables
  • Question: Is treatment duration related to aggression levels?

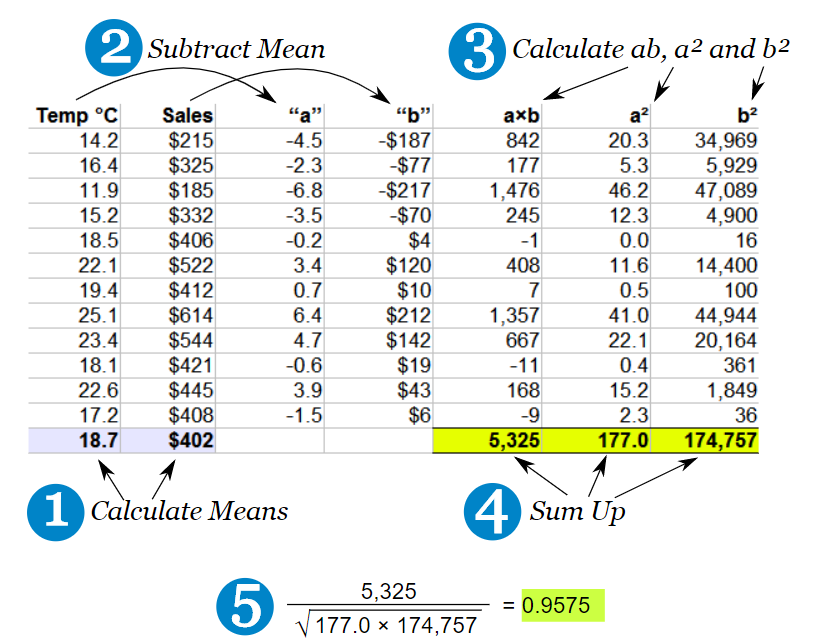
7.2 How is correlation calculated?

  • Think of this as covariance divided by individual variance
  • If the changes are consistent with both variables, the final value will be higher

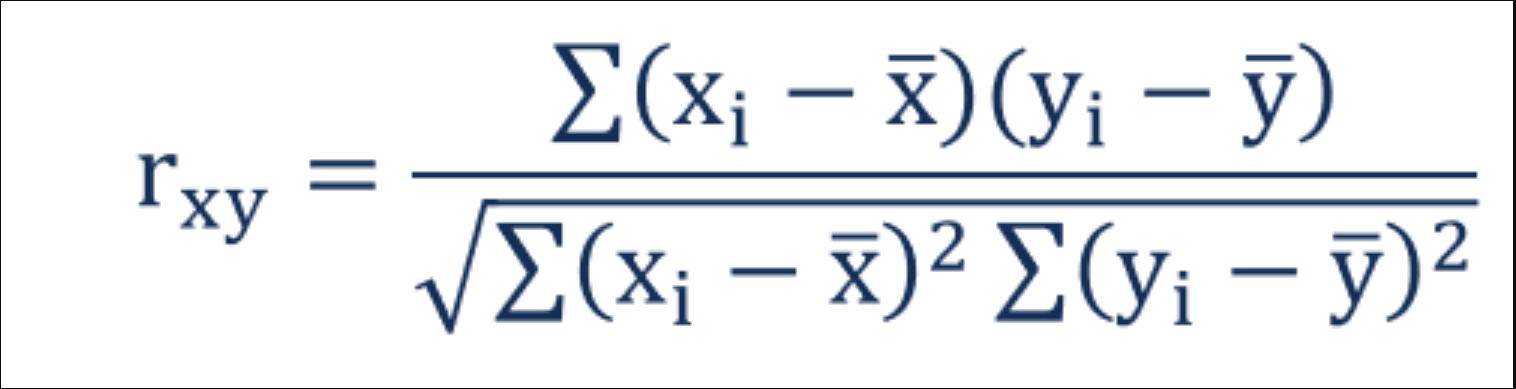
7.3 Running correlation in R

  • Step 1: Check assumptions
    • Data,distribution,linearity
  • Step 2: Run correlation
  • Step 3: Check R value
  • Step 4: Check significance

7.3.1 Check assumptions: data

  • Parametric tests require interval or ratio data
  • If the data are ordinal then a non-parametric correlation is used

What type of data are treatment duration and aggression level?

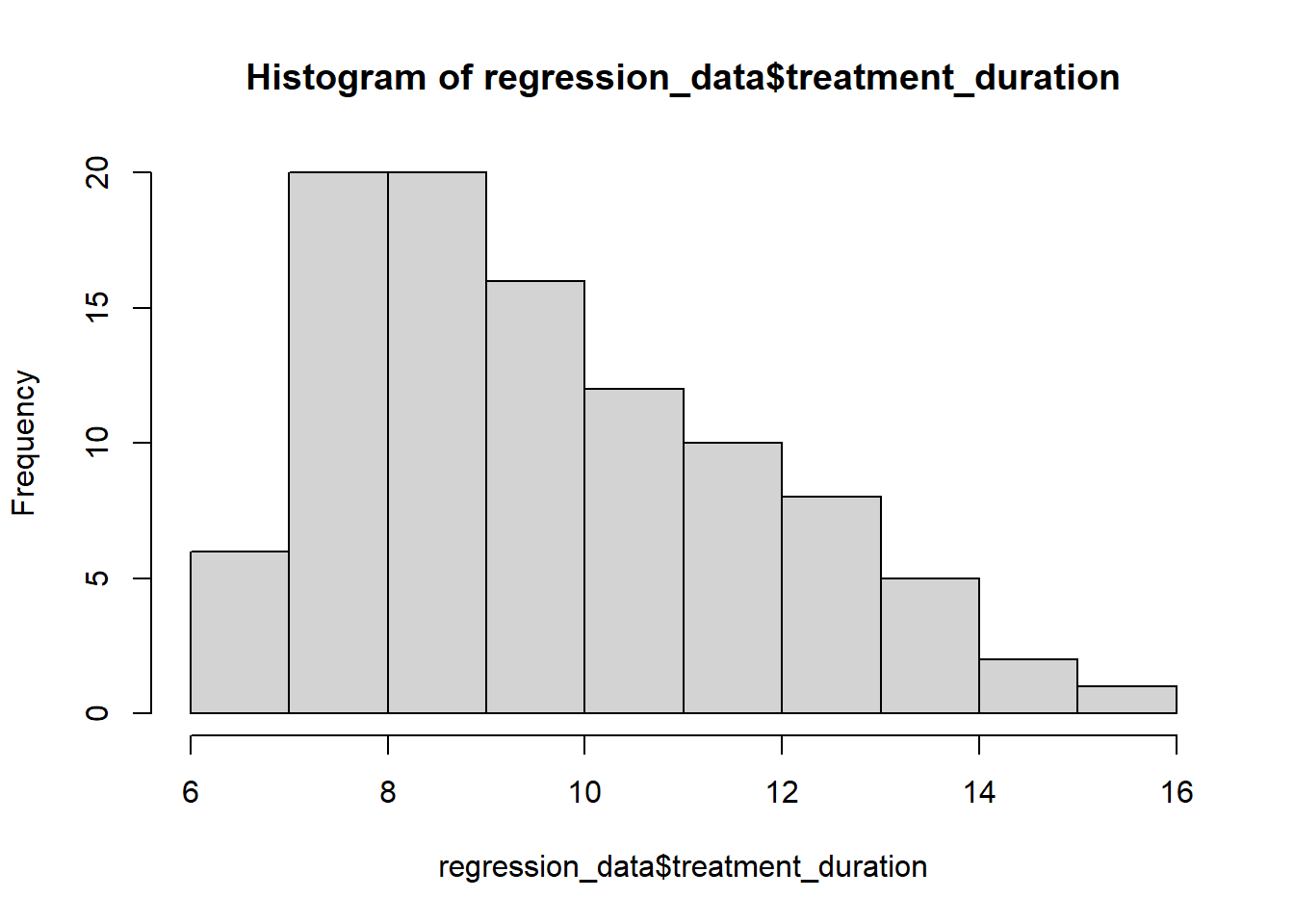
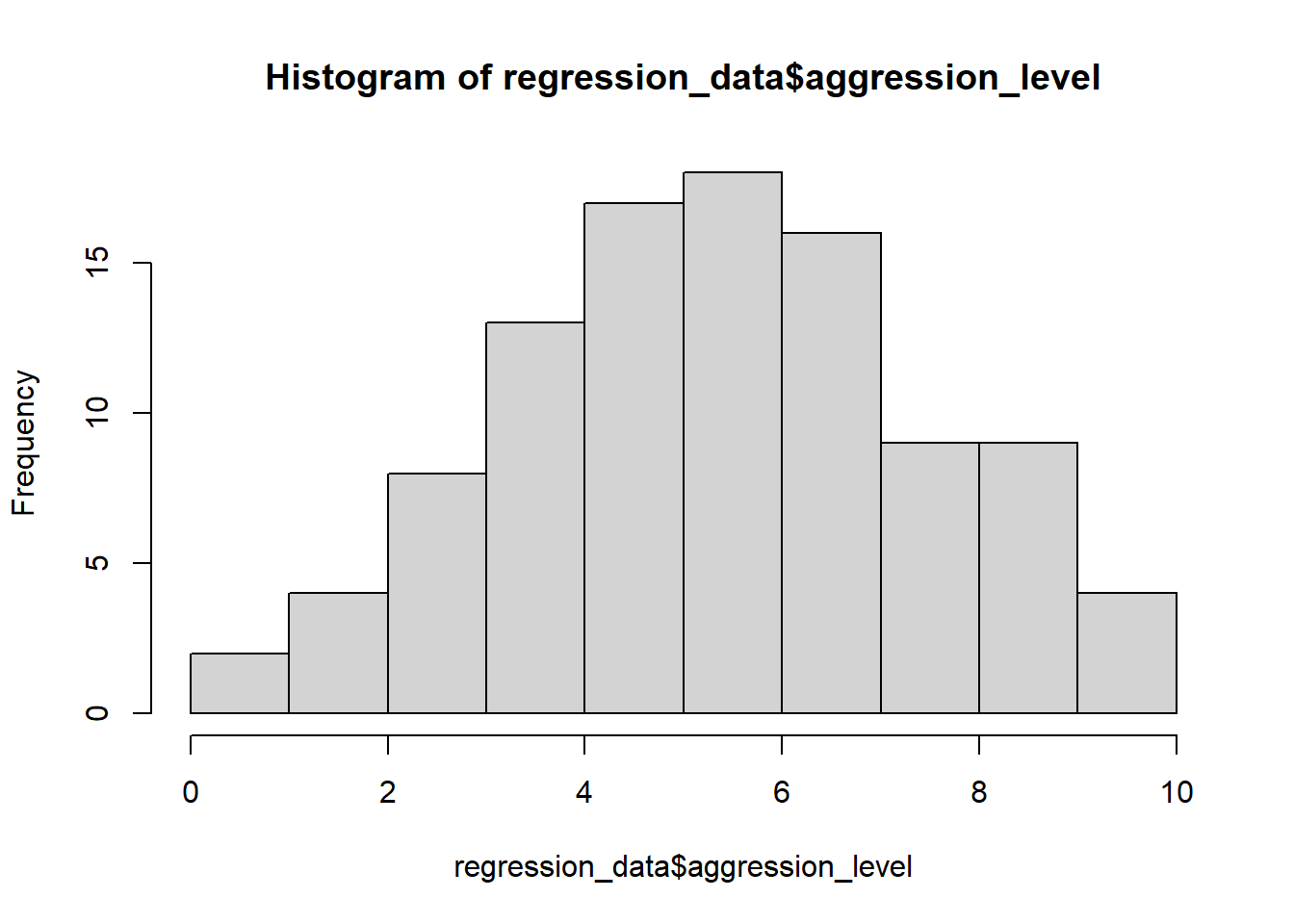
7.3.2 Check assumptions: distribution

  • Parametric tests require normally distributed data

7.3.3 Check assumptions: distribution #2

  • Parametric tests require normally distributed data
shapiro.test(regression_data$treatment_duration)
## 
##  Shapiro-Wilk normality test
## 
## data:  regression_data$treatment_duration
## W = 0.94971, p-value = 0.0007939
shapiro.test(regression_data$aggression_level)
## 
##  Shapiro-Wilk normality test
## 
## data:  regression_data$aggression_level
## W = 0.9928, p-value = 0.8756
  • The normality assumption is less of an issue when sample size is > 30

7.3.4 Checking assumptions: linearity

regression_data %>% ggplot(aes(x=treatment_duration,y=aggression_level)) +
  geom_point()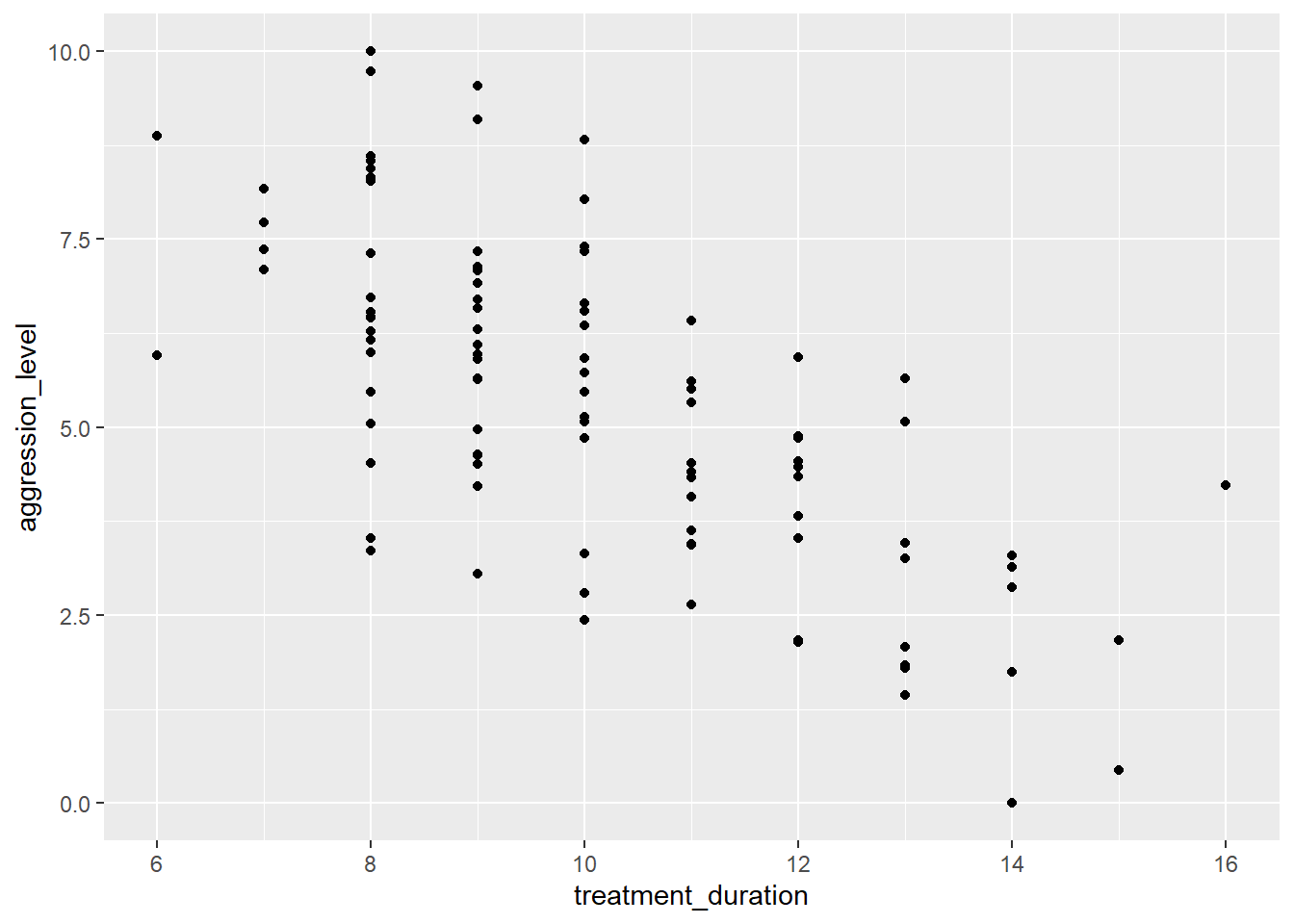

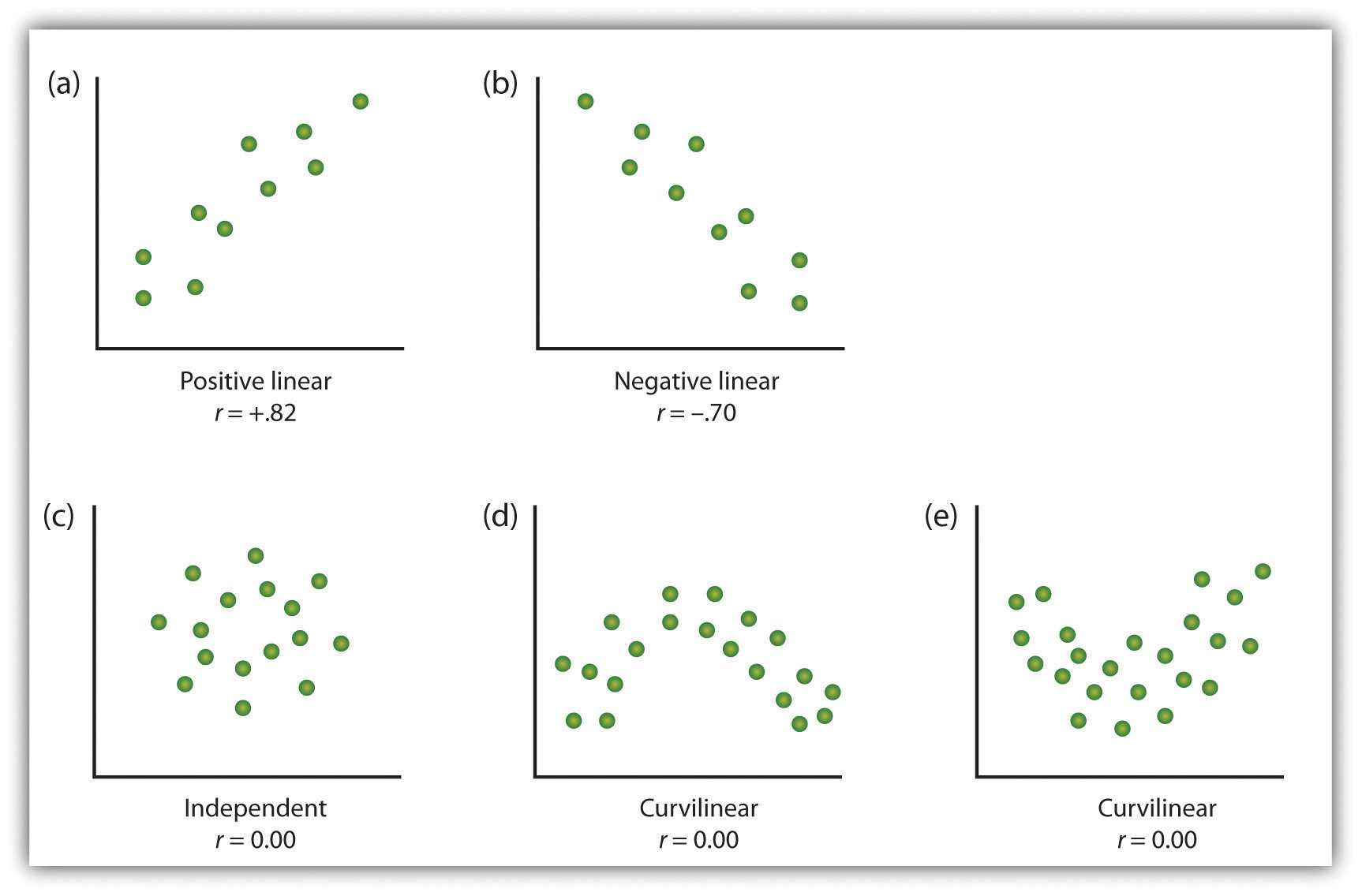
  • Here we are looking to see if the relationship is linear

7.3.5 Run correlation

  • R can run correlations using the cor.test() command
cor.test(regression_data$treatment_duration,regression_data$aggression_level)
## 
##  Pearson's product-moment
##  correlation
## 
## data:  regression_data$treatment_duration and regression_data$aggression_level
## t = -9.5503, df = 98, p-value =
## 1.146e-15
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.7838251 -0.5765006
## sample estimates:
##        cor 
## -0.6942996

7.3.6 Check r Value (correlation value)

  • The r value tells us the strength and direction of the relationship
  • In the output it is labelled as “cor” (short for correlation)
cor.test(regression_data$treatment_duration,regression_data$aggression_level)
## 
##  Pearson's product-moment
##  correlation
## 
## data:  regression_data$treatment_duration and regression_data$aggression_level
## t = -9.5503, df = 98, p-value =
## 1.146e-15
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.7838251 -0.5765006
## sample estimates:
##        cor 
## -0.6942996

7.3.7 Check the significance of the correlation

  • We can see that the significance by looking at the p value
    • The significance is 1.146^-15
    • This means: 0.0000000000000001146
  • Therefore p value < 0.05
cor.test(regression_data$treatment_duration,regression_data$aggression_level)
## 
##  Pearson's product-moment
##  correlation
## 
## data:  regression_data$treatment_duration and regression_data$aggression_level
## t = -9.5503, df = 98, p-value =
## 1.146e-15
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.7838251 -0.5765006
## sample estimates:
##        cor 
## -0.6942996